characteristics of top performances in the women's hammer throw

© by lAAF                  12:2-3; 101-109.1997

Characteristics of top performances in the women's hammer throw:
Basics and technique of the world's best athletes

By Klaus Bartonietz, Lawrie Barclay and Dean Gathercole

" Starting from a presentation of the biomechanical basics of the hammer throw the author characterizes the performance development, performance structure and the technique of Olga Kuzenkova. who was the leading female hammer thrower in 1996, as in previous years. The analysis shows that the world's best female hammer thrower demonstrates a high level of athletic technique although there is still room for further improvement The main requirements for the men's hammer throw are also valid for the training structure of female athletes, i.e. (1) an increase of the training quality (high level of consciousness, execution of the training exercises corresponding with the demands of the target technique), (2) on optimisation of the effects of the yearly training cycle, by varying the components of the training load with regard to volume and intensity, and (3) a balancing of the training loads with restorative and prophylactic measures. "

Dr Klaus Bartonietz is a throws coach and works as a biomechanics expert at the Olympic Training Centre Rheinland-Pfalz/Saarland Schifferstadt, Germany.

Lowrie Barclay is a hammer throw coach (coach of Debbi Sosimenko) at the State Sports Centre Homebush, Sydney/Australia.

Dean Gothercole is a biomechanist, working at the Australian Institute of Sport/Sports Sciences
- Biomechanics Deportment, Canberra/Australia.

1     Biomechanical basics of the hammer throw

In the hammer throw, the distance thrown is determined by the velocity of release, the angle of release, the height of release and air resistance, and is represented by the relationship in equation (see also Figure 1, next page).

     D = v₀² / g cos ¥ (¥sin² ¥ 2gh₀ / v₀ ²) ± C [m] (1)

     D = The distance thrown (m) (e.g. between 40 and 70m, Figure 1)
     vo = The velocity of the hammer at the moment of release (t=0), e.g. between 20 and 26m/s, cf. Figure 1
     ao = The angle of release (direction of the velocity at this moment)
     ho = The height of release (approximately at shoulder height)
     g = The acceleration of the Earth (9.81 m/s2)
     C = A factor characterising the influence of air resistance on the distance thrown
         (i) negative factor - decreased distance (windless, headwind)
         (ii) positive factor - increased distance (heavy tail wind)

the most important factor for a long throw is the velocity of release (as a measure of the hammer's kinetic energy). It is one of the factors that can be maximised by the athlete's actions, the other being the angle and height of release. which can have optimal values. Despite the squared effect of release velocity (see equation 1), the linking with other parameters causes a quasi-linear relationship between release velocity and flight distance of the implement in the targeted zone (i.e. from 40 to 70m, see Figure 1).

Analysis has shown that female athletes achieve angles of release of between 29° and 42° (Bartonietz 1994, Hildebrand / Bartonietz 1995, own
unpublished data). However, an angle of approximately 44° is optimal (Tutevich 1967).
Female athletes tend to have a flat release, which could possibly be caused by the unfavourable relationship between the hammer length and
body height (compared to men), and/or by ineffective legwork during the delivery phase, keeping the plane of movement too flat. A
difference of 5° in the angle of release corresponds to a reduction in the distance thrown of approximately 1 m.


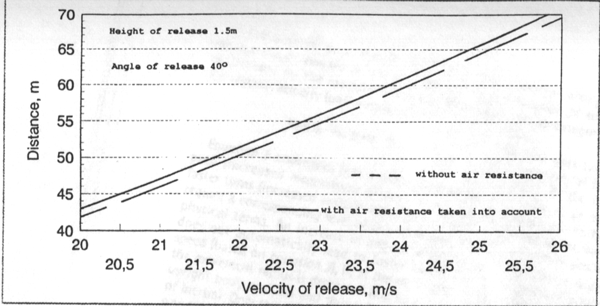
Figure 1: Relationship between velocity of release and the distance thrown in the women's hammer throw

Our analysis shows a tendency towards steeper release angles with increased performance, as shown in the examples below. A highly significant difference between the means of both groups (P<0.001) should be noted here. 20 throws by 13 female athletes in the distance range between 40.50m and 49.64m respectively.
     Average value:         ¥o(av)= 36°
     Standard deviation: ±3.7°
     Minimum value:        ¥o (min) = 29°
     Maximum value:       ¥o (max) = 42°
15 throws by 5 female athletes in the distance range between 50.04m and 67.58m respectively.
     Average value:         ¥o (av) = 40°
     Standard deviation: ±3.0°
     Minimum value:        ¥o (min) = 36°
     Maximum value:       ¥o (max) = 45°

The hammer should leave the hands at the end of the delivery at shoulder level. The height of release is determined by the athlete's physique and technique; i.e., the distance: thrown increases as the height of release increases (Tutevich 1967).

For a throw of 70m with the men's implement, air resistance will reduce the distance thrown by approximately 1.5m (Tutevich 1967). The women's implement has a surface area which is 75% of that of the men's implement. Therefore we can estimate that air resistance may reduce the distance of a throw in the women's event by approximately 1m (windless conditions)

If one considers the physical relationship between linear (vH) and angular velocities (?H) and the radius of the hammer path (rH), it is obvious that the thrower must obtain an optimum relationship between these parameters, which is represented by equation 2 (cf. Figure 2).

     V_H = r_H * ¥_H [m/sec] (2)

If we assume that limits are set for the extension of the radius, an increase in release velocity, e.g. from 22 to 25m/s, is linked with an increase of the (average) angular velocity by 2rad/s (see Figure 2). This will lead to faster turns, with the overall time for the turns being reduced. The data in Table 1 highlight this.

It can be noted that some athletes increase or stabilise the total time taken in the turns (Table 1, part 2). This often leads to an increase in performance. The reason for this phenomenon could hypothetically be that improvements in performance are due to a wider radius of movement (e.g. changes in the duration of the single and support phases). If the athlete reaches a higher velocity of release but the total turning time remains the same (or even slower), then the radius of movement must be wider. This is acceptable, as it indicates that the throwers are utilising all the potential of their technique. Time interval data should not be over-rated. It should be interpreted in combination with information spatial parameters (e.g. radius, body and hammer positions).

Equation 3 demonstrates how the square of the angular velocity (?H) and the radius rH ' affect the centripetal force component (Fcp):

     F_cp = m_h * r_h * ¥_h² [N] (3)

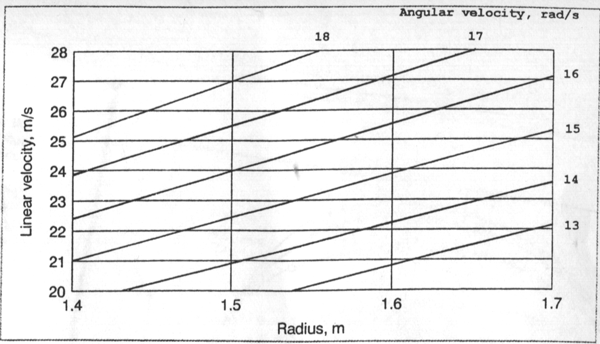
Figure 2:   Relationship between the hammer velocity (vH), radius (rH) and angular velocity (¥H)

Thus there are limits to the amount by which turning speed (angular velocity of the hammer) can be increased. From the thrower's perspective, an increase in the radius seems to be more effective than an increase in angular velocity (i.e. by creating and opening a marked twist between the hip and shoulder axis, as was common for the technical model of the 1970's), because the angular velocity is linked with a squared effect with the centripetal force component (see equation 3).

The velocity of the implement during the turns and at the moment of release is the result of acceleration and deceleration of different parts of the thrower's body. The athlete must transfer a great amount of kinetic energy in short time intervals and must strive for a shortening of braking phases. In other words, she must achieve a corresponding high power level (equation 4).

     power = ¥ energy / ¥ time [kW] (4)

Table 1: Total time for the turns and distance thrown at varying performance levels

Part I

Athlete

Distance [m]

Result
total
duration [s]

<

Result
Distance [m]

Total
duration [s]

Date

Kuzenkova

64.40

2.57

67.58

2.40

25-2-96

63.90

2.46

11-2-96

64.36

2.46

11-2-96

Melinte

66.54

2.18

66.84

2.06

23-5-97

Sosimenko

60 20

1.77

62.70

1.64

25-2-96/11-2-96

59.50

1.70

62.86

1.62

11-2-96

Mathes

48.90

1.64

53.28

1.56

10-7-93
(Bartonietz 1994)

61.24

2.24

63.94

2.16

23-5-97

Beyer

57.50

1.72

60.54

1.66

29-5-96/27-4-96

for comparison:

Sedykh

75.40

1.60

82.34

1.47

(Bartonietz 1994)

82.34

1.47

84.92

1.43

Weis

74.66

2.23

79.20

2.13

14-5-94/28-7-91

75.06

2.18

14-5-94

Sidorenko

78.22

2.12

80.64

2.06

6-6-92

Part II

McNaugthon

52.66

2.25

55.28

2.28

26-1-96

56.00

2.38

11-2-96

Mathes

54.60

2.30

57.36

2.28

14-5-94

for comparison:

Weis

77.72

2.22

80.46

2.22

6-6-92

76.12

2.16

60.52

2.16

3-6-97

Sidorenko

76.32

2.04

60.76

2.02

3-6-97

In the case of a rotational movement, the average power exerted on the implement (PH) is determined by the moment of inertia (IH) and the
angular velocity (?H) - equation 5.

     P_H = l_H * ¥_H [kW] (5)

Equation 5 underlines that a wider movement path (increased momentum of inertia) and/or faster turns (increased angular velocity) basically
require a corresponding level of driving power in physical terms. An increase in angular velocity does not automatically lead to faster hammer speed (based on equation 3), if, at the same time, the movement radius is decreased (e.g. by a more upright body position and thus a lower moment of inertia). Only the necessary power level, developed by special training, can guarantee the effective interaction between movement path (radius) and angular velocity.

2     Characteristics of Olga Kuzenkova's technique

Olga Kuzenkova was the leaning female hammer thrower in 1996, as in previous years. Her result of 69.46m, set on 2nd February 1996 at
the Sydney International Athletic Centre in Homebush, was a World's best performance. Table 2 shows her performance development over
the years.

Her performance structure is characterised by her best weightlifting results of:
Full squat   150kg
Clean       100kg
Snatch     70kg

Olga's best performance in the shot put is over 16m. Her first hammer competition was at the national championships in Russia. at the age of
19, where she recorded a throw of 45m. She has forecast that a throw of at least: 75m will be the winning mark at the 2000 Olympics (Barclay
1996).

Table 2: Performance development of Olga Kuzenkova, Russia

Born: 4 October 1970. body mass 70kg. arm span 1.77m

Year

Result

1990

59.34m

1991

61.52m

1992

65.40m

1993

64.54m

1994

66.54m

1995

68.75m

1996

69.46m

1997

73.40m

Her technique is an example an almost perfect implementation of the tars-c. technique, in general, with great emphasis being placed on the
function of support and drive. Olga's technique can be categorised by the following characteristics:
(i) She uses two preliminary swings (as do the majority of female and male hammer throwers). At the high point of the second swing                           there is an active turn of the upper body towards the hammer, to sweep the implement to the front. The low point is reached at a 7     o'clock position.
(ii) She uses a wide initial stance (47% wider than her shoulder width) as she goes into the first turn. The distance between the feet decreases from the stance at the start (0.55m) up to the delivery (0.37m) by about 35% (see Figure 3),

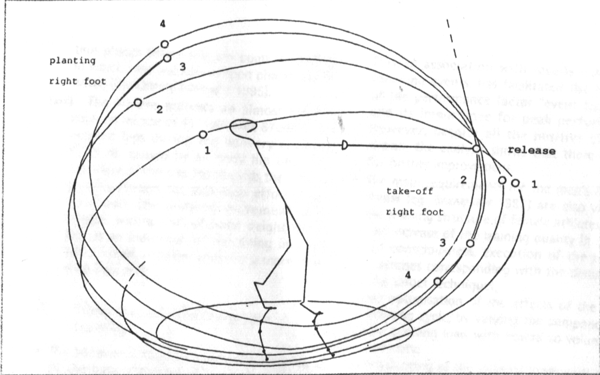
Figure 3:   Trajectory of the hammerhead and hammer positions at the moment of take-off and right foot plant - view from behind: Olga Kuzenkova, 66.00m 30 June 1995, St. Petersburg/Russia

(iii) From turn to turn, a shortening of the duration of the single support phase occurs, with the double support phases being longer than the single support phases (see Table 3). This influences the performance, in that the best throws are characterised by the shortening of the single support phases in favour of the double support phases (Figure 4).

Table 3: Duration of leg work phases of Olga Kuzenkova's throws

66.OOm 30-June-95 Goodwill-Meeting St. Petersburg

duration of phases [s]

turn

single

double

Interval "right foot
Plant – left heel down"

1

0.30

0.50

0.24

2

0.26

0.30

0.18

3

0.24

0.26

0.18

4

0.22

0.30

0.12

67.58m Optus Grand Prix Hobart 25-Feb-96

duration of phases [s]

turn

single

double

1

0.30

0.50

2

0.23

0.35

3

0.24

0.23

4

0.25

0.30

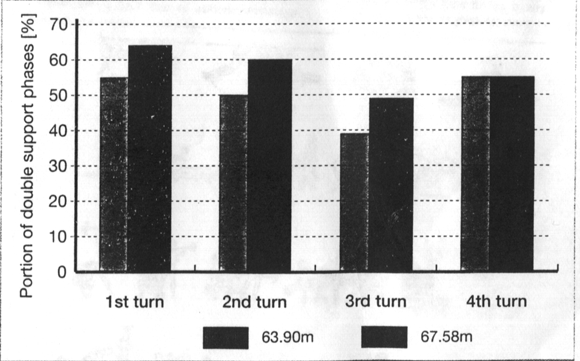
Figure 4:   Portion of the double support phases of the time interval for each turn (duration of single support + duration of double support 100%)
Throws of Olga Kuzenkova, Optus Grand Prix, Hobart, Australia 25 February 1996

(iv) Going into the first turn relatively late (at a 2:30 o'clock position), the head is leading the movement. Looking at the head of the hammer would be more effective for a wide hammer movement and a fast turn under the hammer (out-run). The arms are elevated, reducing the radius (note the broken line "shoulders-grip-hammer head" in Figure 4). Figure 4 compares her body positions going into the first turn with the target position. Using the target position, the athlete could gain additional centimetres of radius, maintaining this advantage up to the last turn.
(v) During the four turns, at the moment of right foot plant, the angle of twist between hip and shoulder axis reached almost 40°. This occurred due to the wide path of the hammerhead and the fast turn of the right leg around the left. In comparison, in Sedykh's world     record throw of 86.74m, accomplished with 3 turns, at the moment of right foot plant, there was a difference in the shoulder and hip     rotation of 50°.
(vi) The early catch of the hammer:
1st turn 10:30 o'clock position,
2nd turn 10 o'clock position,
3rd and 4th turns - 11 o'clock position
Figure 3 shows the trajectory of the hammer movement. A negative aspect of this throw is that the double support phase of the second turn starts relatively late (67.SBms late at the beginning of the double support phase of the 3rd turn). A fast plant of the left heel occurs (see Table 3), before the low point of the hammer's trajectory is reached, with effective working of the right against the stable left side (driving the upper body plus the triangle "shoulder axis-grip").

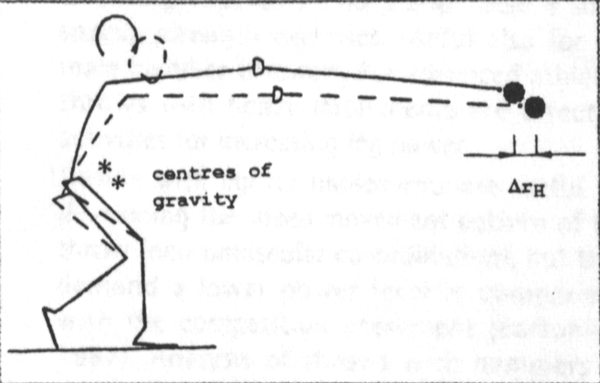
Figure 5:   Body position going into the first turn: Olga Kuzenkova, 66.OOm (full lines) and body position of the target technique (broken lines)
Note: The body position of the target technique is characterised by a lower centre of gravity.

(vii) At the low points no more twist occurs, but there is a "tracking angle" (see Figure 6). and the hip and shoulder axis are almost parallel. This shows that the legs are the effective "engine" for driving the implement through the low points of it's trajectory (except for the 3rd turn, see Figures 3 and 6). Often both female and male athletes finish the acceleration phases before the low point is reached, in which case two acceleration phases can be noted (Hildebrand/Bartonietz 1995).
(viii) The athlete achieves an almost optimal angle of release of 41° (distance 67.58m). The crossed legs during the delivery (66.00m, 67.58m), caused by an early hip and knee extension of the free leg towards the ground, possibly hinders the maximum effort of the final pull.     The jumping movement after release, with a shift of body weight to the left, is an indication of remaining impetus, which could be better used for a more powerful final pull.

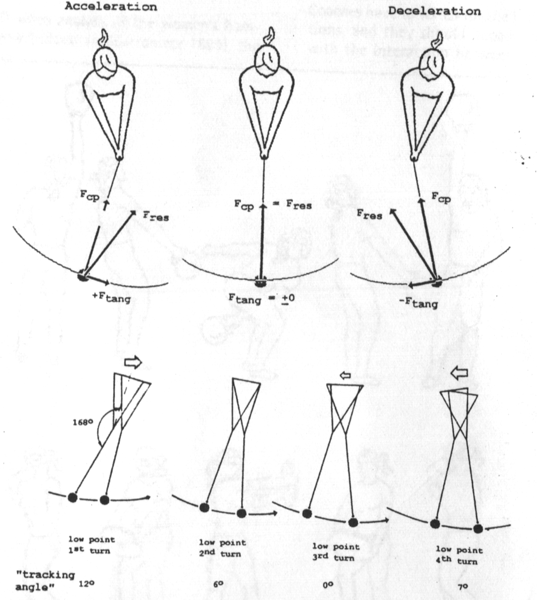
Figure 6:   The main phases of the hammer throw (Bartonietz 1987, above) and positions of the hammer, arms and shoulder axes at the low points of the hammer's trajectory, Olga Kuzenkova, throw of 66.00m 30 June 1995 (below)
Note: An angle between the hammerhead, grip and middle of the shoulder axis of <180° points to acceleration (e.g. of 168°, 1st turn: The "tracking angle" is determined by 180° - 168° = 12°). The arrows above the shoulder axis snow the direction of movement of the shoulder girdle.

3              Summary and conclusions for training

The permanent development of the knowledge of the basic elements of the hammer throw technique (the correct internal image of the     technique) is a must for both coaches and athletes. This study will attempt to give guidance to coaches and athletes to help them obtain the necessary basic and special knowledge, as a background for the analysis of the technique and the planning of the training load of their own athletes.

The world's best female hammer thrower demonstrates a high level of athletic technique. This, in association with results from other throwing events, has facilitated the targeting of the performance factor "event technique" and its importance for peak performances. However, despite all the positive elements shown, the analysis shows that there is room for further improvement.

The main requirements for the men's hammer throw (e.g. Bakarynov 1987) are also valid for the training structure of female athletes, ie:
-   an increase of the training quality (high level of consciousness, execution of the training exercises corresponding with the demands of the target technique),
-   an optimisation of the effects of the yearly training cycle, by varying the components of the training load with regard to volume and      intensity.
-   a balancing of the training loads with restorative and prophylactic measures. In the hammer throw there exists an inseparable relationship between technique and performance; the perfection of technique has to be a full year task. Any strength increase must comply with the demands of technique (special training on a year-round basis). Unity of skill and capacity is the leading principle of strength and technique training.

The event-specific kind of leg power, in terms of physics, is the crucial element in hammer throwing. Figures 7 and 8 and Table 4 show special strength exercises, useful also for female hammer throwers. For advanced athletes, throws with heavy implements are effective activities for increasing leg power. Throws with lighter implements are useful for developing the speed movement pattern of the throw (neuromuscular co-ordination), but they demand a lower power level in comparison with the competition implement (Bartonietz 1987). Analysis of throws with hammers of various lengths and masses seems to show the same results for men as for women. However, the specific movement pattern of throws with implements of different masses and lengths does not automatically cause the necessary changes required for improvement of the competition throws. The intended changes happen only after consideration of the technique of throws with different implements (Bartonietz 1987).

From 3D-video analysis of the women's hammer throw (Hildebrand/Bartonietz 1995), the following recommendations car be given:
-   Strive for a wide movement path of the implement going into the first turn (based on a flexible shoulder axis with a full extension of      the arms).
-   Keep the body low going into the first turn and subsequent turns, to create a wide movement path of the implement and a powerful leg extension during the delivery. Being too upright seems to be the result of insufficient specific leg and trunk power.
-    Before increasing maximum strength level, try for effective use of the current physical ability in the necessary body positions (special strength exercises): use drills (e.g. multiple swings and turns with weights of different forms and masses) and simulations, in order to feel comfortable in the position. This is necessary to avoid a gap between physical ability and skill.
-   Coaches have to watch for the key body positions, and they should become acquainted with the interaction between thrower and      hammer. Familiarisation with the transference of momentum between athlete and implement (redistribution of rotational energy) is      essential.

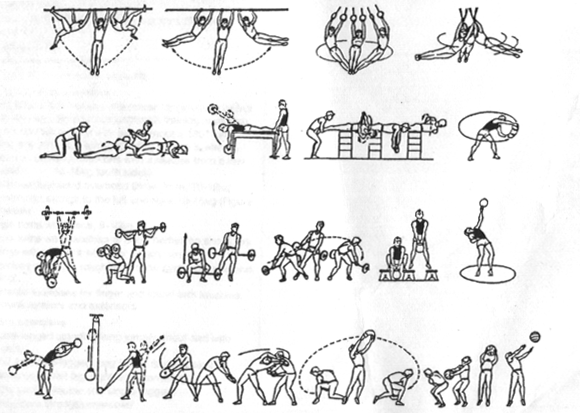
Figure 7: Special strength training exercises for female hammer throwers (Bondarchuk 1985, Voronkin, Limar 1989, adapted)

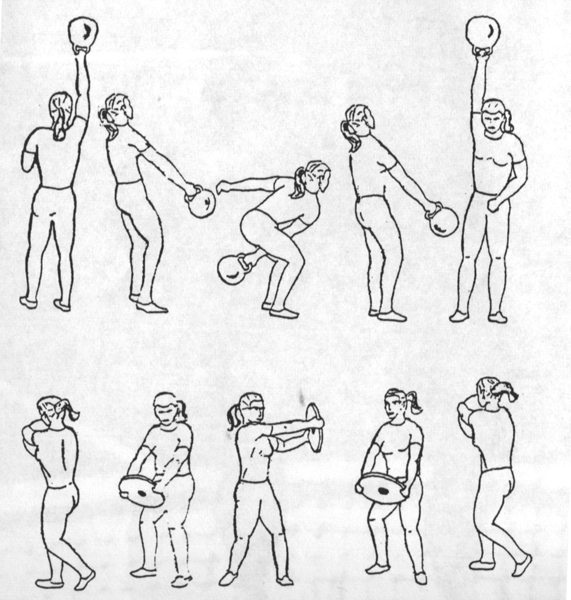
Figure 8:   Special strength exercise for female hammer throwers )ARBEIT et al. 1988, adapted) above: high kettlebell swings with 180° turn, below: barbell disk swings

Table 4: The main training exercises for female hammer throwers

Throwing movements

competition implement (4kg/1.19m)

- full number of turns

- reduced number of turns (working on a powerful delivery)

light hammers 3.5kg and 3kg/1.19m

heavy hammers 4.5kg, 5kg/1.19m and slightly shorter (l.l5m-1.17m)

heavy shortened hammers thrown from 2-3 turns

6kg/1.10-1.00m

7.26kg/0.80m

throws with weighted belts

throws with ankle/lower leg cuffs

Special strength exercises

simulations with the use of a mirror for position control

(can also be abused during strength training sessions)

high kettlebell swings with and without a 180° turn,

using one and both arms, 10-15kg (Figure 8, above)

kettlebell delivery imitations with a release from a low position, 0-15kg (both sides)

kettlebell backward overhead throw from, 10-15kg

barbell disc swings to the left and right 10-15kg (Figure 8. below)

single turns with discs, 5-10kg

single turns with sandbag or short barbell on shoulders

swings left and right with 1 or 2 hammers

exercises on pulley machines (in the gym, standing and sitting)

isometric exercises for finger and lower-arm muscles, for trunk rotators and extensors

Jumping exercises

double-legged standing long jump(without and with weights)

3 and 4 double-legged long jumps (bunny hops)

multiple hops (left leg, right leg, alternating)

hurdle jumps (double and single-legged)

Main maximum strength exercises

squat (back, front, double and single-legged)

high pulls (clean grip and snatch grip)

snatch (from floor and hang)

clean

REFERENCES

ARBEIT, E.; Bartonietz, K.; Börner, P.; Brandt, K.; Dörr, A.; Goldmann, W.; Hellmann, K.; Hillebrandt, L.; Hinz, L.; Hofmann, S.; Lunau, G.; Köllner, J.; Riedel, B.; Rietschel, M.; Schattke, U.; Schotte, K.-H.; Thomas, B.:
Erhöhung der wirksamkeit des Einsatzes spezieller Kraftübungen zur Entwicklung wurfapezifischer Kraftfähigkeiten. Research Institut for
Sports (FKS), Leipzig, 1988, 132 pp. (unpublished research report)

Bakarinov, Y.:
Metanie molota: Evoluzija i perspectivy [Hammer throw: evolution and perspectives]. In: Legkaya Atletika (1987), 1, pp. 12-14

Barclay, L.:
Olga Kuzenkova's Australian visit In: Modern Athlete and Coach 34 (1996), 4, pp. 36-37

Bartonietz, K.:
Zur sportlichen Technik der Wettkampfübungen und zur Wirkungsrichtung ausgewählter Trainingsübungen in den Wurf- und
Sto?disziplinen der Leichtathletik [The technique of competition exercises and the effect of selected training exercises in the throwing events
and shot put]. postdoctoral thesis, Leipzig: DHfK, 1987

Bartonietz, K.:
Biomechanical analysis of throws with hammers of various weight and length as basis for an effective training. In: Brüggemann, G.-P.; Rühl,
J.K. (eds.): Techniques in Athletics, 1st International Conference, Cologne 7-9 June 1990, vol. 2 Free Communication Sessions, 1990, pp.
542-551

Bartonietz, K.:
Hammerwurf der Frauen - quo vadis? In: Die Lehre der Leichtathletik 33 (1994), 3, pp. 15-16, 33-34; 4, p.18

Hildebrandt, F., Bartonietz, K.:
Eine biomechanische Analyse des Hammerwerfens am Beispiel der Technik zweier Werferinnen. In: IAT e.V. Leipzig (ed ): Schriftenreihe zur angewandten Trainingswissenschaft 3 (1995), 2, pp. 45-56

Bondarchuk, A.P.:
Metanie Molota [Hammer throw], Moscow, 1985

Otto, R.:
NSA Photosequence 22 - Hammer Throw:' Yuriy Sedykh 86.74w, Commentary. In: New Studies in Athletics, 7
(1992), 3, pp. 51-65

Voronkin, V.I.; Limar, P.L.:
Melanie molota [Hammer throw]. In: Legkaja Atletika, Moscow 1989, pp. 590-607